Feb 8, 2018 at 9:26 AM
Join Date: May 6, 2009
Location: somewhere new
Posts: 2135
Age: 30
Pronouns: he/him
Abstract
Typically the detune effect found in the Org Maker program is used for subtractive synthesis, a means for creating a more complex sound with two slightly out of tune notes played in unison. I was curious if the function could also be used to properly tune notes in a single chord song to account for equal temperament tuning found in all electronic instruments.
---
Background
The frequency of a sound wave determines the pitch of a note. When increasing the number of half-periods in a set distance (ie decreasing the wavelength), the harmonic series precipitates. In order of increasing periods we get: the fundamental, perfect 5th, perfect 4th, major 3rd, minor 3rd, and so on.
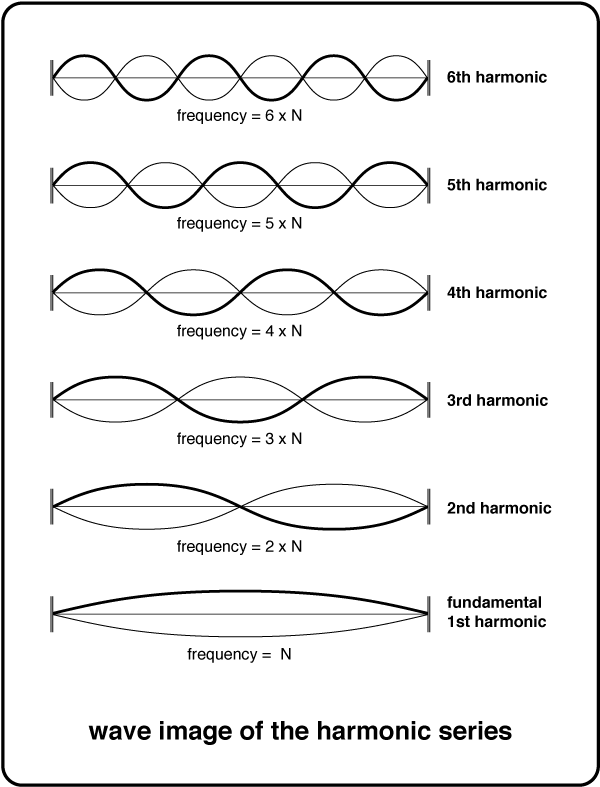
In order to create a smooth sound, stringed instruments typically tune a single string to a set frequency, then simply tune the other strings based on the first string's vibrations. This ensures that most chords being played will be free of beat interference.
However, for instruments with too many strings (pianos) or digital instruments, this tuning is impossible. Instead, the octave (containing 12 half-steps) is divided into 12 even intervals, one for each note. This is called equal tempered tuning. Equal tempered tuning is a solid approximation in most cases, but playing what should be a perfectly harmonious chords like a major triad will always cause beat interference.
---
Methods
I began by creating a spreadsheet with the differences between equal tempered and pure intonation (sometimes called "just" temperament):
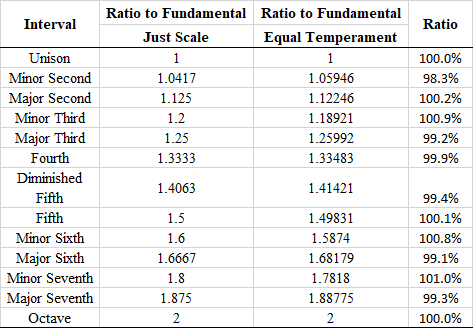
And wrote a simple one chord track in organya:

---
Results
The single note change (from minor 7th to major 6th) constitutes the highest change in error for any two intervals (a difference of 1.9%), and was thusly excluded from study. I recorded the chord from both files and opened them in a waveform analysis program:
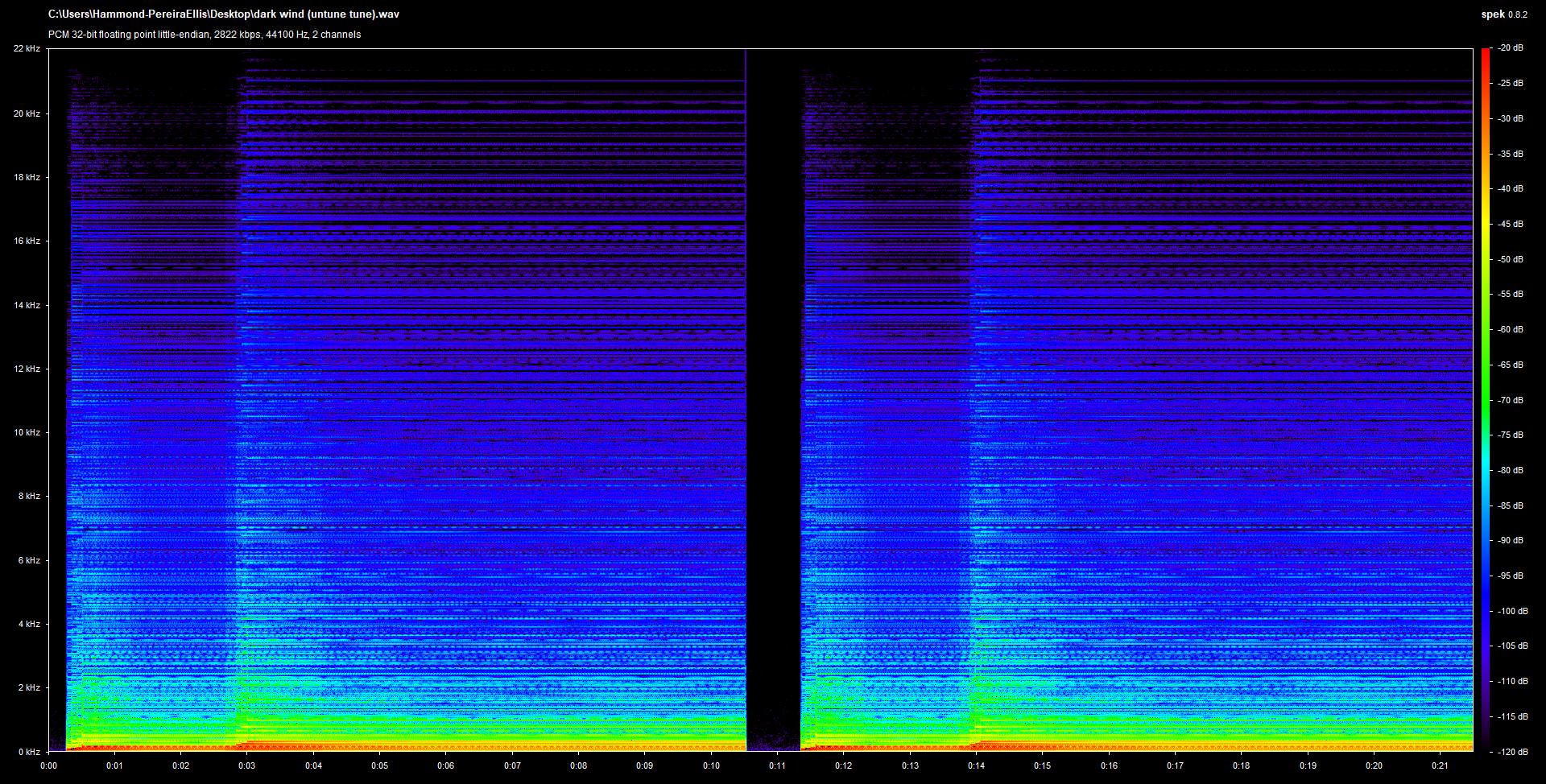
The image was cleaned, inverted to increase contrast, and superimposed using subtractive layer blending.
Subtracting equal temper from just:
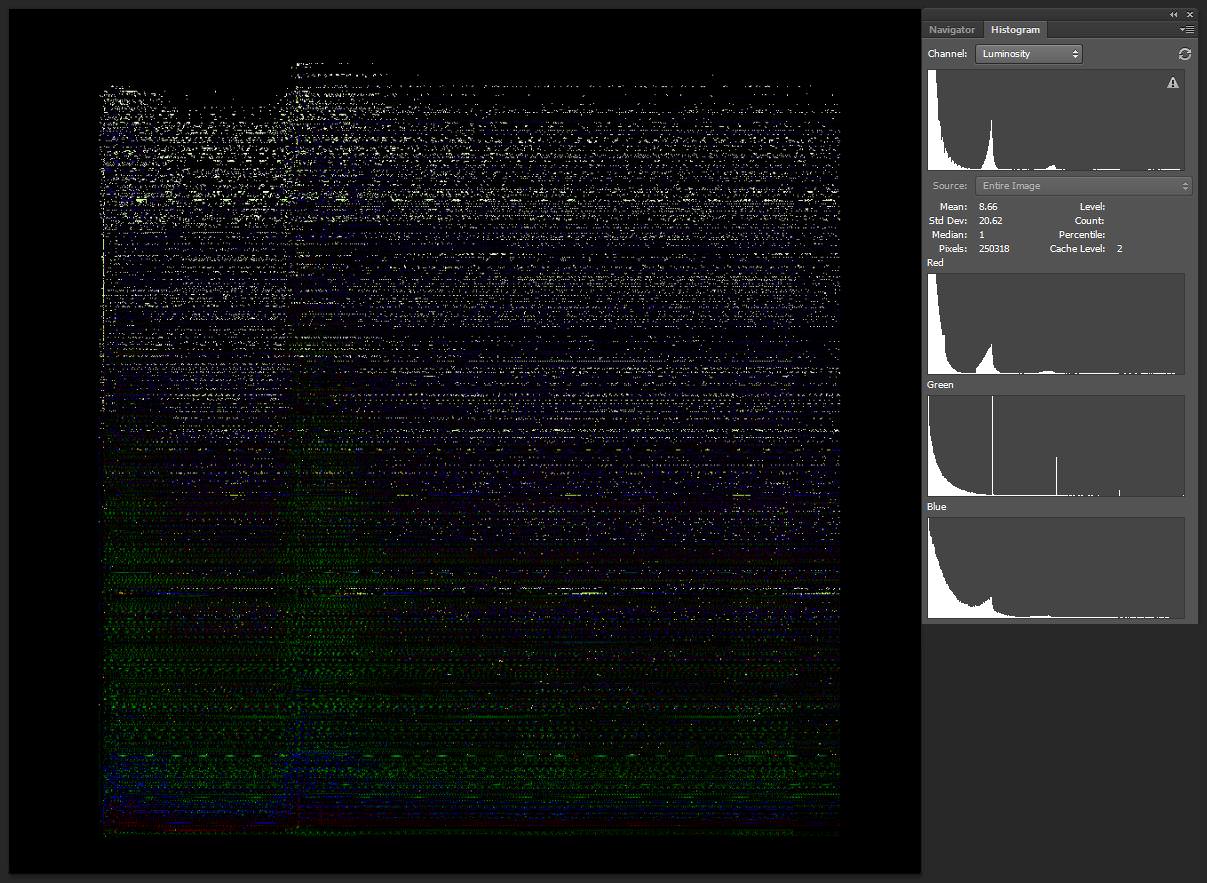
Subtracting just temper from equal:
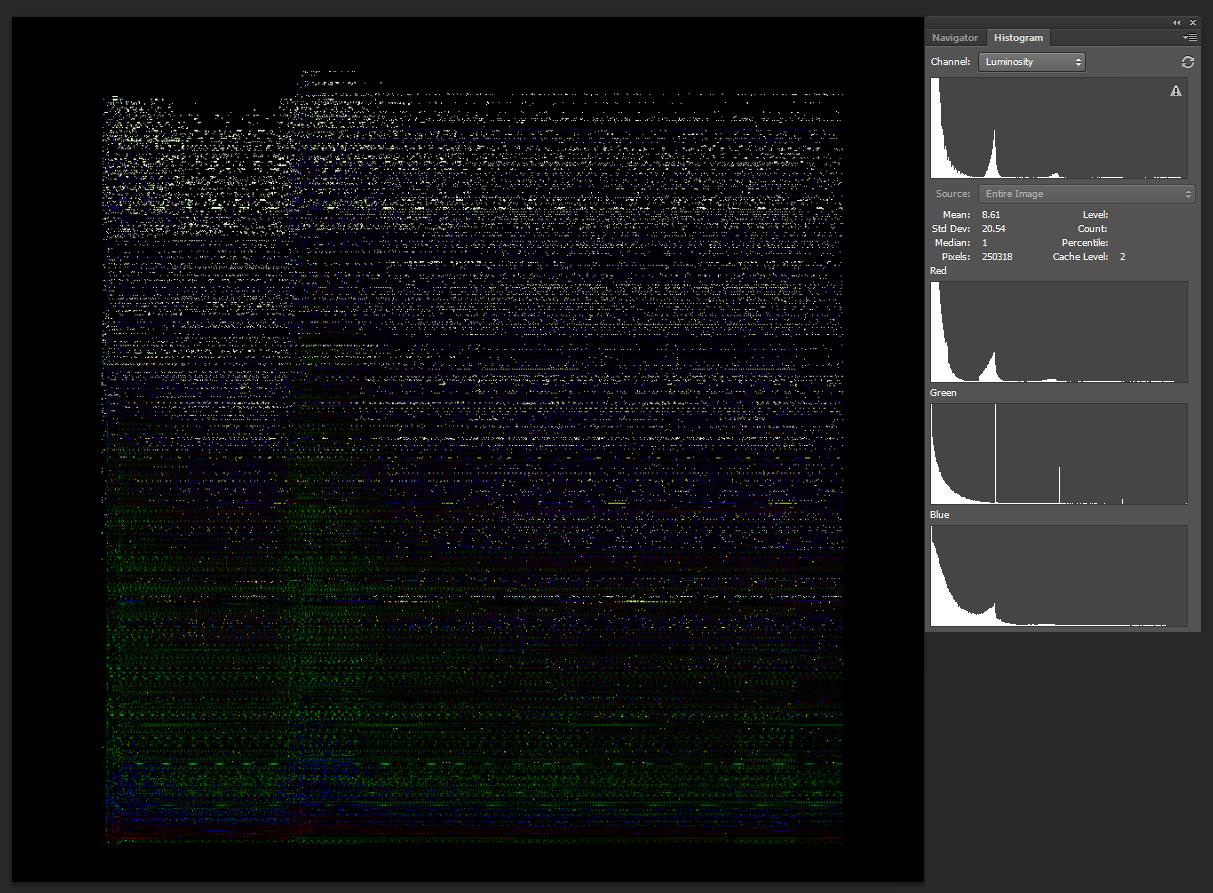
It appears there is negligible difference between the two, based on the luminosity histograms. I am looking into more sophisticated methods of analysis (that don't cost $100) and will post updates here if I make substantial progress.
Until then, can you hear the difference? I'd like to think the just temper sounds less prone to beats but that's easily placebo.
Typically the detune effect found in the Org Maker program is used for subtractive synthesis, a means for creating a more complex sound with two slightly out of tune notes played in unison. I was curious if the function could also be used to properly tune notes in a single chord song to account for equal temperament tuning found in all electronic instruments.
---
Background
The frequency of a sound wave determines the pitch of a note. When increasing the number of half-periods in a set distance (ie decreasing the wavelength), the harmonic series precipitates. In order of increasing periods we get: the fundamental, perfect 5th, perfect 4th, major 3rd, minor 3rd, and so on.

In order to create a smooth sound, stringed instruments typically tune a single string to a set frequency, then simply tune the other strings based on the first string's vibrations. This ensures that most chords being played will be free of beat interference.
However, for instruments with too many strings (pianos) or digital instruments, this tuning is impossible. Instead, the octave (containing 12 half-steps) is divided into 12 even intervals, one for each note. This is called equal tempered tuning. Equal tempered tuning is a solid approximation in most cases, but playing what should be a perfectly harmonious chords like a major triad will always cause beat interference.
---
Methods
I began by creating a spreadsheet with the differences between equal tempered and pure intonation (sometimes called "just" temperament):

And wrote a simple one chord track in organya:

---
Results
The single note change (from minor 7th to major 6th) constitutes the highest change in error for any two intervals (a difference of 1.9%), and was thusly excluded from study. I recorded the chord from both files and opened them in a waveform analysis program:

The image was cleaned, inverted to increase contrast, and superimposed using subtractive layer blending.
Subtracting equal temper from just:

Subtracting just temper from equal:

It appears there is negligible difference between the two, based on the luminosity histograms. I am looking into more sophisticated methods of analysis (that don't cost $100) and will post updates here if I make substantial progress.
Until then, can you hear the difference? I'd like to think the just temper sounds less prone to beats but that's easily placebo.
Last edited:

